回归分析(英语:Regression Analysis)是一种统计学上分析数据的方法,目的在于了解两个或多个变数间是否相关、相关方向与强度,并建立数学模型以便观察特定变数来预测研究者感兴趣的变数。更具体的来说,回归分析可以帮助人们了解在只有一个自变量变化时因变量的变化量。一般来说,通过回归分析我们可以由给出的自变量估计因变量的条件期望。–维基百科
1. 简介
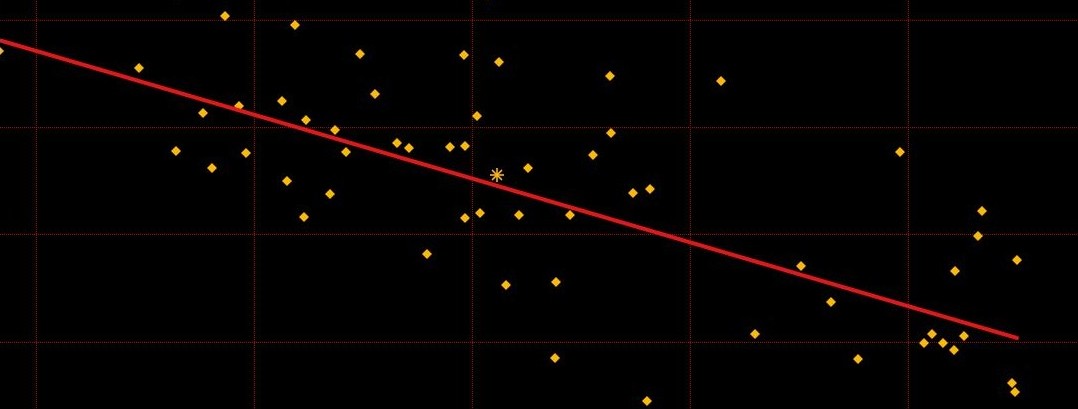
回归分析是一种预测性的建模技术,它研究的是因变量(目标)和自变量(预测器)之间的关系。这种技术通常用于预测分析、时间序列模型以及发现变量之间的因果关系。回归分析是建模和分析数据的重要工具。在这里,我们使用曲线/线来拟合这些数据点。在这种方式下,从曲线或线到数据点的距离差最小。
回归分析的原理:通过找出一条最能够代表所有观测资料的函数(回归估计式)来表示因变数与自变数之间的关系。
回归分析的好处:
- 它表明自变数与因变数之间的显著关系;
- 它表明多个自变数对一个因变数的影响强度;
- 它允许我们比较哪些衡量不同尺寸的变量之间的互相影响,比如价格变动与促销活动数量之间联系。这些有利于帮助市场研究人员、数据分析人员以及数据科学家排除并估计出一组最佳的变量,用来构建预测模型。
2. 回归模型
回归模型主要包括以下变量:
- 未知参数,记为$b$,可以代表一个标量或一个向量;
- 自变量,$X$
- 因变量,$Y$
回归模型将$Y$ 和一个关于$X$ 和$b$的函数关联起来:
$$Y=f(X,b)$$
回归问题的条件:收集的数据和假设的模型。该模型即为一个函数,这个函数里面含有未知的参数,通过学习,可以估计这些参数,然后利用这个模型去预测/分类新的数据。
3. 回归分析的种类
有各种各样的回归技术用于预测。这些技术主要有三个度量(自变量的个数、因变量的个数以及回归线的形状)。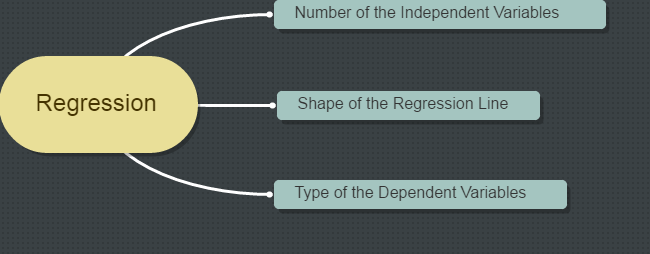
3.1 线性回归 Linear Regression
在统计学中,线性回归(Linear regression)是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为简单回归,大于一个自变量情况的叫做多元回归。
在线性回归中,数据使用线性预测函数来建模,并且未知的模型参数也是通过数据来估计。这些模型被叫做线性模型。最常用的线性回归建模是给定X值的y的条件均值是X的仿射函数。不太一般的情况,线性回归模型可以是一个中位数或一些其他的给定X的条件下y的条件分布的分位数作为X的线性函数表示。像所有形式的回归分析一样,线性回归也把焦点放在给定X值的y的条件概率分布,而不是X和y的联合概率分布(多元分析领域)。
在线性回归技术中,因变量是连续的,自变量可以是连续的也可以是离散的,回归线的性质是线性的。线性回归使用最佳的拟合直线(也就是回归线)在因变量(Y)和一个或多个自变量(X)之间建立一种关系。用一个方程式来表示为:
$$Y=a+b \cdot X+e$$
上式中,a表示截距, b表示直线的斜率, e表示误差项。这个方程可以根据给定的预测变量X来预测目标变量的值。下图是线性回归的图形显示: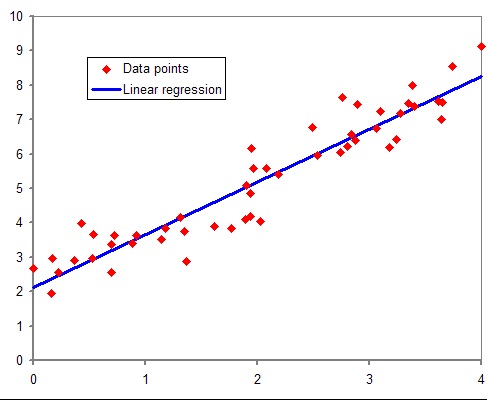
线性回归的求解方法可以使用最小二乘法。
3.2 逻辑回归 Logistic Regression
逻辑回归(英语:Logistic regression 或logit regression),即逻辑模型(英语:Logit model,也译作“评定模型”、“分类评定模型”)是离散选择法模型之一,属于多重变量分析范畴,是社会学、生物统计学、临床、数量心理学、计量经济学、市场营销等统计实证分析的常用方法。
逻辑回归是用来计算“事件=success”和“事件=failure”的概率。当因变量的类型属于二元(1/0,真/假,是/否)变量时,我们就应该使用逻辑回归。这里,Y的值从0到1,可以用下面的方程表示:
$$
odds= p/ (1-p) = probability of event occurrence / probability of not event occurrence\
ln(odds) = ln(p/(1-p))\
logit(p) = ln(p/(1-p)) = b_0+b_1X_1+b_2X_2+b_3X_3….+b_kX_k$$
上述式子中,$p$表述具有某个特征的概率。
3.3 多项式回归 Polynomial Regression
(To be continued)
3.4 逐步回归 Stepwise Regression
(To be continued)
3.5 岭回归 Ridge Regression
(To be continued)
3.6 套索回归 Lasso Regression
(To be continued)
3.7 ElasticNet回归
(To be continued)
参考:
